논문 링크(967 인용)

쉬운 목차

요약

본 논문에서 제안하는 mf는 기존 방법과 달리 암시적 피드백을 사용하지만 관찰되지 않은 피드백에 다른 가중치를 부여한다. 아이템 인기도를 반영하는 가중치입니다.
또한 eALS는 기존의 ALS 방식을 시간복잡도 측면에서 개선하여 온라인 추천이 가능하도록 제안한다. 기존 방식에 비해 복잡도가 K배 향상되었음을 보여준다.
온라인 추천을 지향하기 때문에 사용자와 아이템 간의 상호작용 데이터를 실시간으로 받아 업데이트할 수 있는 방법을 제시한다.

동기 부여

암시적 피드백을 사용하는 mf는 일반적으로 사용자 x 항목 행렬의 모든 값을 사용하지만 누락된 값에 동일한 가중치를 부여합니다.
그러나 이러한 모델 가정은 현실과 거의 일치하지 않습니다. 이는 관찰되지 않은 상호 작용이 모두 동일한 가중치를 갖지 않기 때문입니다. 어떤 항목은 너무 인기가 많아서 사용자가 발견하지 못했을 수도 있고 다른 항목은 인기가 없어서 사람들이 피했을 수도 있습니다.
이러한 현실적인 가정을 반영하기 위해 본 논문에서는 암시적 피드백을 사용하여 mf를 수행할 때 결측값에 대해 서로 다른 가중치를 가정한다. 이 경우 item-popularity가 사용됩니다.
또한 암시적 피드백을 사용하면 모든 데이터가 학습에 사용됩니다. ALS는 많은 계산이 필요하지만 여전히 오랜 시간이 걸리는 SGD를 대체하기 위해 제안되었습니다. 이 문제를 해결하기 위해 기존 mf보다 K배 빠른 eALS를 제안합니다.

접근하다

암시적 피드백을 위한 MF 방법

$\mathbf{R}\in \mathbb{R}^{M\times N}$
M 사용자, N 항목
$\mathcal{R}$: 0이 아닌 (사용자, 항목) 쌍
$\mathbf{p}_u, \mathbf{q}_i$: 사용자 u 및 항목 i에 대한 잠재 벡터
$\mathcal{R}_u$: 사용자 u와 상호 작용하는 항목 집합
$\mathcal{R}_i$: 항목 i와 상호 작용하는 사용자 집합

mf는 $\mathbf{R}$의 $r_{ui}$를 사용자와 항목 간의 내적 및 사용자/항목의 편향 항으로 예측하려고 합니다.

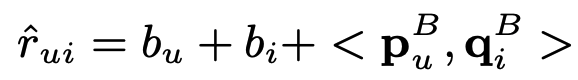
아래 손실을 최소화하여 모델 매개변수를 학습합니다.

'추천 관련글,

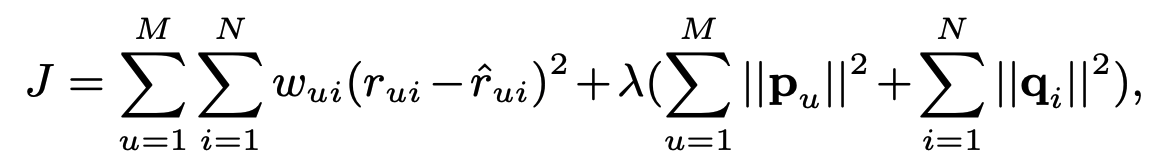
암시적 피드백이 사용되기 때문에 모든 데이터에 대한 용어가 있습니다(합계는 M 및 N에 대한 것임).
$w_{ui}$: 사용자별, 아이템별로 다르게 부여되는 가중치입니다. 일반적으로 상호 작용 수의 함수로 정의되며 신뢰도라고 합니다.

ALS에 의한 최적화

모델 매개변수에는 $\mathbf{p}_u 및 \mathbf{q}_i$의 두 가지 유형이 있습니다. ALS의 핵심 아이디어는 그것들을 동시에 해결하는 것이 아니라 하나를 고정시키면서 다른 하나를 차례로 최적화하는 것입니다. 먼저 $\mathbf{p}_u$에 대한 최적화를 진행하기 위해서는 다음과 같이 $\mathbf{p}_u$와 관련된 용어만 남겨둔다.

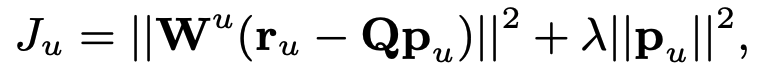
자세히 보면 가중 능선 회귀의 한 형태입니다. 즉, $|| \mathbf{W} ( \mathbf{y} – \mathbf{X \beta} ) ||^2 + \lambda || \mathbf{\beta} ||^2$는 이에 대한 솔루션을 쉽게 도출할 수 있습니다.

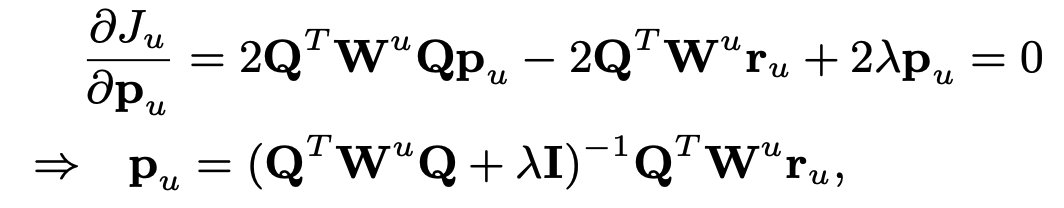
\mathbf{q}_i에 대한 식도 같은 방식으로 도출할 수 있습니다.

ALS는 $K \times K$ 행렬의 역행렬을 찾아야 하기 때문에 $O(K^3)$ 시간이 걸립니다. 또한 행렬 $\mathbf{Q}^T \mathbf{W}^u$는 $K \times N$와 $K \times K$의 행렬 곱이므로 $O(NK^2)$ 시간. . 종합하면 한 사용자에 대한 매개변수 업데이트의 시간 복잡도는 $O(K^3 + NK^2)$입니다. M 사용자의 경우 $O(M(K^3 + NK^2))$, N명의 사용자에 대해 $O(N(K^3 + MK^2))$이므로 $O((M+N)K^3 + MNK^ 2)$. 데이터의 크기가 크면 당연히 부담이 됩니다.

균일한 가중치로 속도 향상

높은 시간 복잡도를 줄이기 위해 누락된 값에 동일한 가중치 $w_0$를 부여하는 것이 제안됩니다. 이를 이용하면 다음과 같이 표현을 단순화할 수 있다.

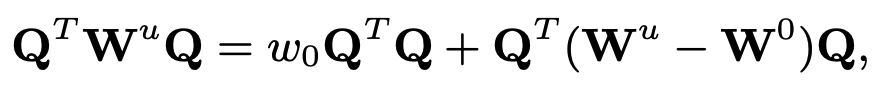
$w_0 \mathbf{Q}^T \mathbf{Q}$: u에 의존하지 않으므로 미리 계산할 수 있습니다.
$\mathbf{W}^u – \mathbf{W}^0$: $N \times N$이지만 0이 아닌 항목이 $|\mathcal{R}_u|$만큼 많습니다. 항의 수는 $| \mathcal{R}_u|$. 여기서 주목해야 할 중요한 점은 $N >> |\mathcal{R}_u|$입니다.
$\mathbf{Q} \in N \times K$ $\mathbf{Q}^T (\mathbf{W}^u – \mathbf{W}^0) \mathbf{Q}$는 $O(K이므로 ^2N)$가 아닌 $O(K^2|\mathcal{R}_u|)$의 시간 복잡도를 갖습니다. $N >> |\mathcal{R}_u|$ 때문입니다.
M명의 사용자와 N개의 항목을 반복하면 시간 복잡도는 $O((M+N)K^3 + |\mathcal{R}| K^2)$입니다.
이는 대용량 데이터에 ALS를 적용하기에는 여전히 어려운 시간 복잡도입니다. 또한 등가중이라는 것 자체가 가정이라는 사실 자체가 현실과 동떨어져 있다.

일반 요소별 ALS 학습기

ALS 솔루션에는 몇 가지 병목 현상이 있었으며 그 중 하나는 역행렬을 계산하는 것이었습니다. 이것은 매개변수가 벡터 단위로 업데이트되기 때문에 발생하므로 본 논문에서는 요소 단위로 매개변수를 업데이트한다. 다음과 같이 $p_{uf}$에 대한 도함수를 유도해 봅시다.

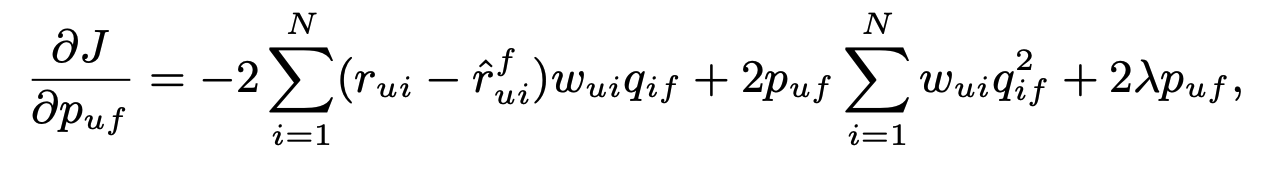
$\hat{r}^f_{ui} = \hat{r}_{ui} – p_{uf} q_{if}$. 이제 이것을 0으로 설정하고 닫힌 솔루션을 얻습니다.

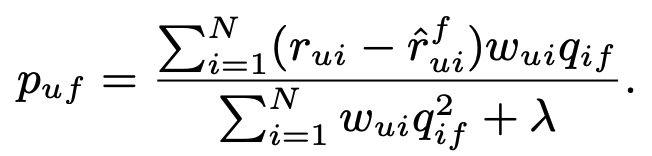
$q_{if}$도 비슷하게 얻을 수 있습니다.

시간 복잡도를 계산해 봅시다. 각 반복 라운드에서 원시 구현의 복잡성은 $O(MNK^2)$입니다. 그 이유는 다음과 같습니다.

$\hat{r}^f_{ui} = \hat{r}_{ui} – p_{uf} q_{if}$ 및 $\hat{r}_{ui} = b_u + b_i + \sum_f p_ {uf}q_{if}$. 따라서 여기서 발생하는 시간 복잡도는 $O(K)$입니다. $\hat{r}_{ui}$를 미리 계산할 수 있다면 시간복잡도는 $O(1)$로 줄일 수 있다.
분자가 N개의 항을 더하기 때문에 시간 복잡도는 $O(N)$이고 분모도 마찬가지입니다.
따라서 하나의 $p_{uf}$를 계산하는 시간 복잡도는 기껏해야 $O(N)$입니다.
신중하게 생각해보면 $p_{uf}$에는 총 K개의 요인과 M명의 사용자가 있습니다. 따라서 전체 요소별 잠재인자를 계산하는 시간복잡도는 $O(MNK)$이다.
$q_{if}$에 대한 시간복잡도도 $O(MNK)$로 나오므로 총 시간복잡도는 $O(MNK)$가 된다.
역행렬을 수행하지 않기 때문에 시간이 크게 단축되며 $\hat{r}_{ui}$를 미리 계산하면 시간을 더 줄일 수 있다.

제안된 암시적 방법: 누락된 데이터에 대한 항목 지향 가중치

논문은 암묵적 피드백의 결측값에 동일한 가중치를 부여하는 것은 비현실적인 가정임을 지적하고 다음과 같은 목적함수를 제안한다.

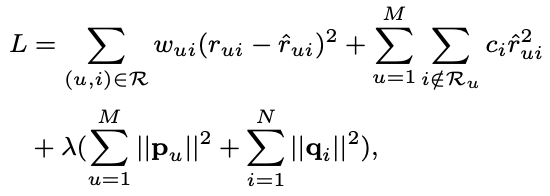
가중치 $w_{ui}$는 관찰된 암시적 피드백 $\mathcal{R}$에만 할당됩니다.
항목 중심 가중치 $c_i$는 각 사용자에 대해 누락된 값이 있는 데이터($i \notin \mathcal{R}_u$)에 할당됩니다.
두 번째 항인 $\sum_u \sum_{i \notin \mathcal{R}_u} c_i \hat{r}^2_{ui}$는 암시적 피드백을 모델링하기 위해 풀어야 하는 항입니다.

대중성을 고려한 가중치 전략

사용자가 선택한 항목은 아니지만 해당 항목이 인기가 있으면 향후 사용자가 선택할 가능성이 높습니다. 이러한 생각을 반영한 가중치는 다음과 같습니다.

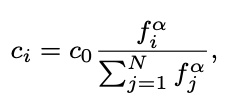
$f_i$: 항목 i의 인기도, $|\mathcal{R}_i| / \sum_{j=1}^N \mathcal{R}_j$.
$c_0$: 누락된 값의 전체 가중치.
$\alpha$: 이 매개변수는 인기 있는 항목과 인기 없는 항목 사이의 인기도를 조정합니다.

빠른 eALS 학습 알고리즘

eALS를 통한 $p_{uf}$는 다음과 같이 업데이트됩니다.

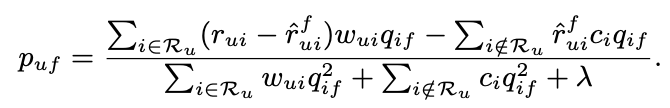
여기서 병목 현상은 $\sum_{i \notin \mathcal{R}_u}$와 관련이 있습니다. 왜냐하면 모든 부정 샘플이 반환되어야 하기 때문입니다. 먼저 분자 부분을 살펴보겠습니다.

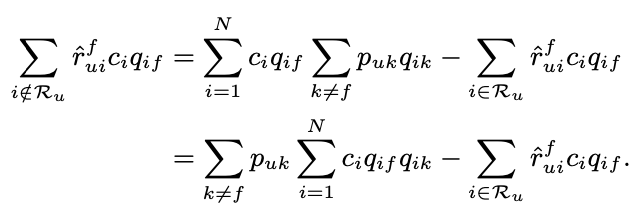
표기법에 유의하십시오. $\mathbf{p}_u = ( \mathbf{p}^B_u, b_u, 1 )^T$ 및 $\mathbf{q}_i = ( \mathbf{q}^B_i, 1, b_i )^T$ . 따라서 $p_{uk}$에는 모든 바이어스 항이 포함됩니다.
이렇게 식을 확장하면 병목이 되는 부분이 $\sum^N_{i=1} c_i q_{if} q_{ik}$임을 알 수 있다.
본 논문에서는 연산량을 줄이기 위해 $\mathbf{S}^q = \sum^N_{i=1} c_i \mathbf{q}_i \mathbf{q}^T_i$를 메모한다.

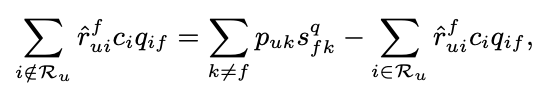
이것은 $O(K + |\mathcal{R}_u|)$의 시간 복잡도로 계산됩니다. 마찬가지로 분모는 cahe를 다음과 같이 적용합니다.

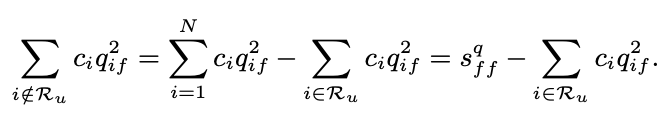
이를 종합하면 $p_{uf}$에 대한 업데이트는 다음과 같이 진행될 수 있으며, 시간 복잡도는 $O(K + |\mathcal{R}_u|)$, 즉 $O(MNK)$이다. 기존 암시적 피드백 방식. 상당한 개선이 있음을 알 수 있다.

시간 복잡도 분석

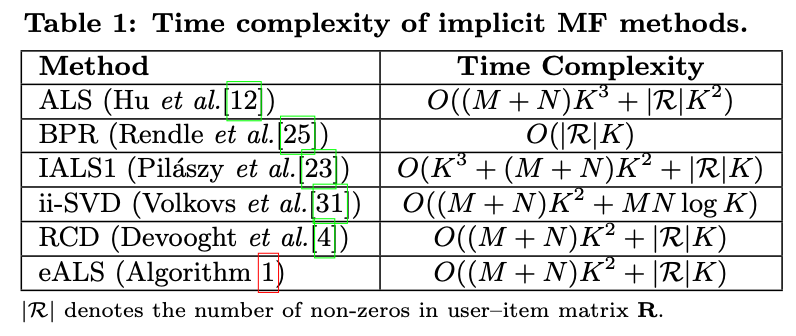
ALS 대 eALS: eALS가 K배 빠름
ii-SVD 대 eALS: eALS가 더 빠름
RCD vs eALS: 시간 복잡도는 동일하지만 RCD는 학습률 조정이 필요합니다.
BPR vs eALS: BPR의 시간 복잡도는 낮지만 BPR은 양의 피드백만 사용하고 누락된 값은 사용하지 않습니다.

결과

오프라인 프로토콜

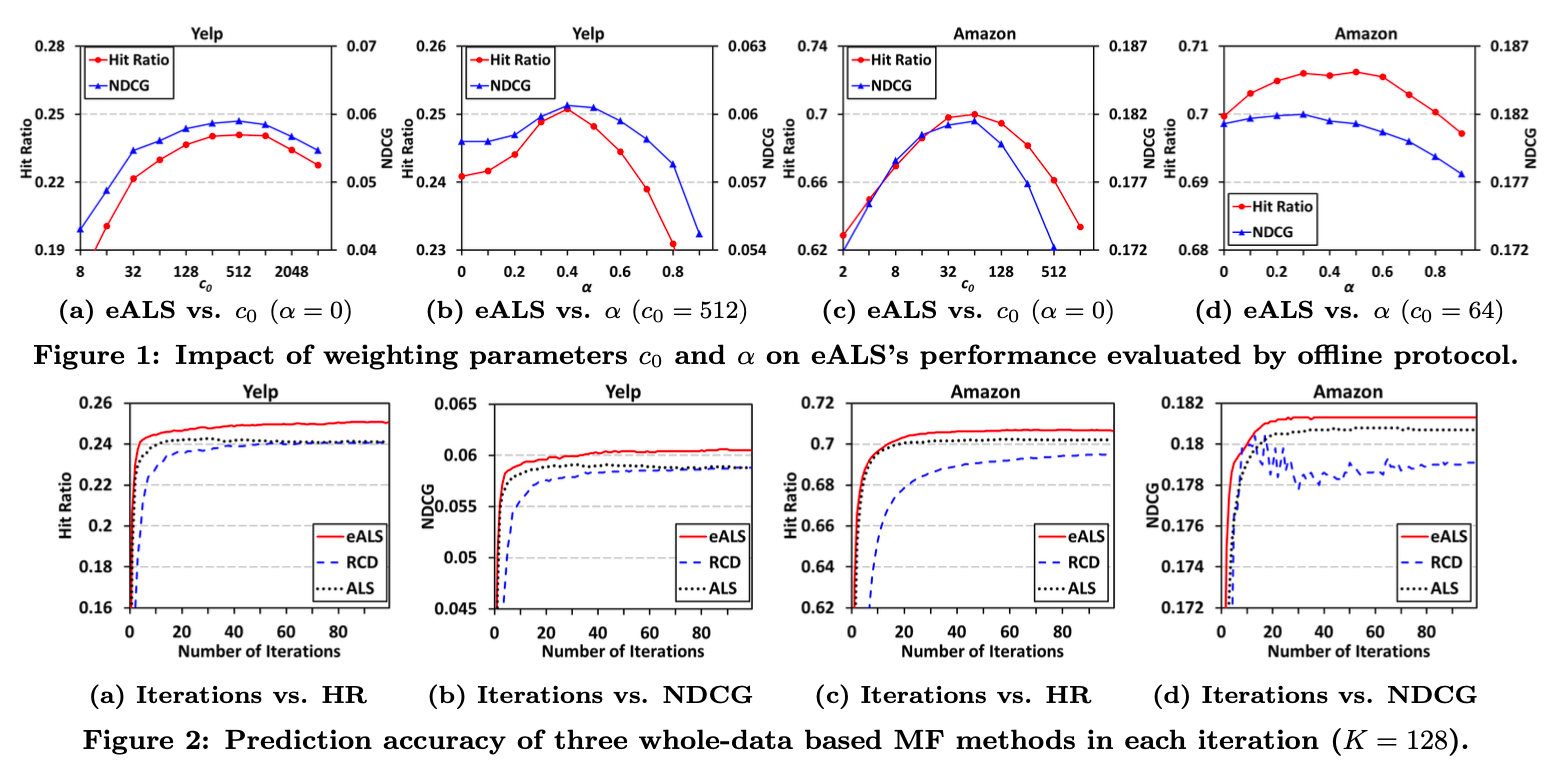
그림 1
- 두 데이터셋에서 최적의 $c_0, \alpha$를 찾기 위한 실험이다.
- $\alpha$는 일반적으로 0.4정도를 최적점으로 판단하였고 $c_0$은 서로 상이하였다.
그림 2
- eALS vs RCD vs ALS 실험 결과입니다.
- 반복에 관계없이 eALS가 지속적으로 더 높은 성능을 보이는 것을 알 수 있습니다.

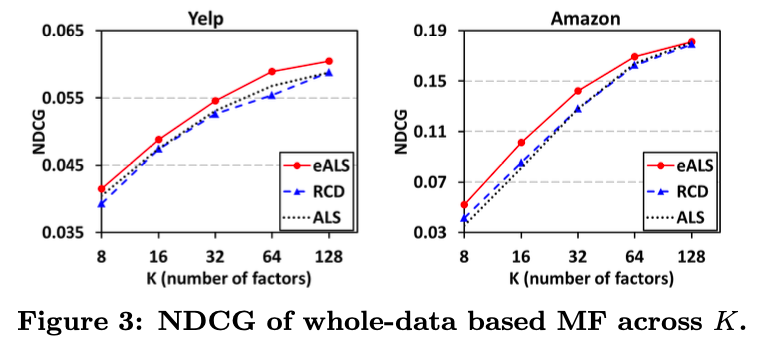
요인의 수에 따른 평가지표의 변화에 관한 실험이다.
요인의 수가 증가할수록 일반화가 향상되고 성능이 향상됨을 알 수 있습니다.

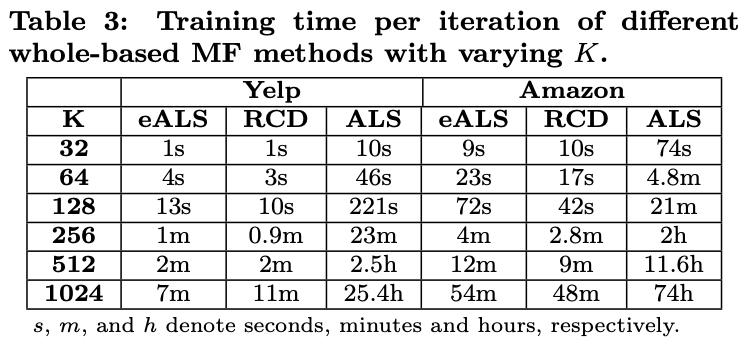
분석적으로 계산했을 때 eALS와 RCD의 시간 복잡도는 비슷했고 ALS의 시간 복잡도는 K배 더 컸다.
행렬 곱셈을 구현한 라이브러리는 시간복잡도를 최적화하지만 K배만큼은 아니지만 요인의 수가 늘어날수록 ALS가 학습하는데 많은 시간이 걸린다는 것을 알 수 있다.
일반화는 데이터가 많은 상황에서 중요하며, 모델이 일반화를 잘 하기 위해서는 과적합되지 않는 방향으로 K를 증가시켜야 합니다. 이런 환경에서 K가 크면 학습 시간이 오래 걸린다는 점은 치명적일 수 있어 eALS의 장점을 다시 한 번 확인할 수 있다.

온라인 프로토콜

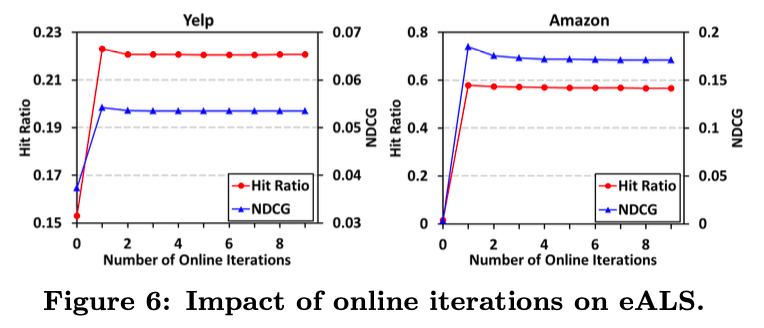
온라인 반복 횟수에 따른 성능 비교 실험입니다.
적은 반복 횟수로도 성능이 빠르게 수렴되는 것을 알 수 있습니다.

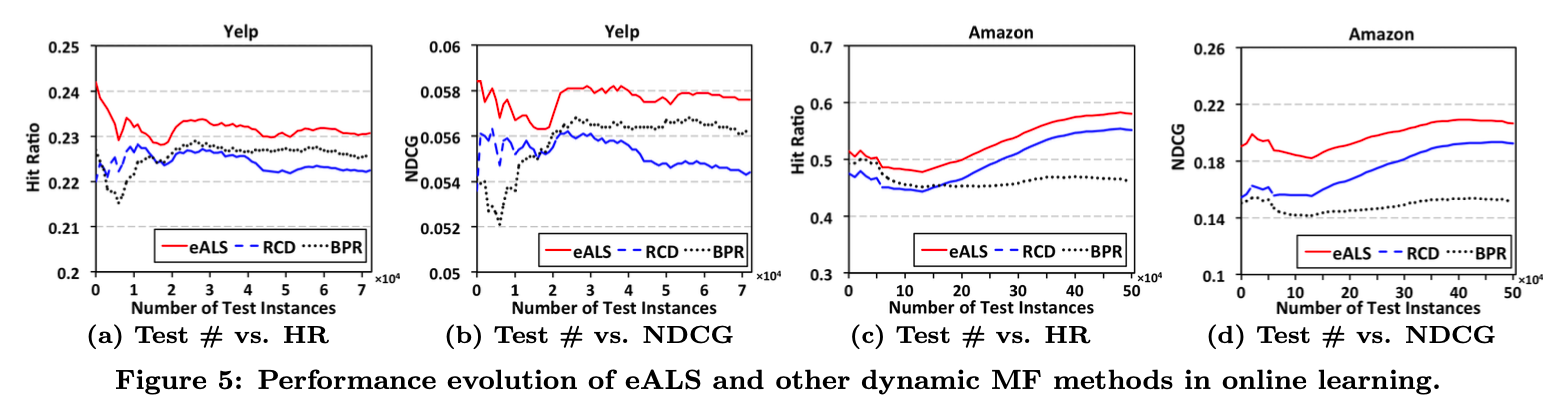
테스트 데이터 개수에 따른 온라인 학습 성능을 비교하는 실험입니다.
테스트 횟수가 적든 많든 eALS가 다른 모델에 비해 좋은 성능을 보인다는 것을 알 수 있습니다.

결론

MF에 대해 많은 것을 배울 수 있는 논문이었습니다. 특히 이 논문은 2016년에 발표되었지만 MF에 feature를 넣는 것에 대해 많은 연구가 이루어진 것 같고, 빠르게 학습하는 알고리즘에 대한 필요성이 있는 것 같습니다.
이를 위해서는 시간복잡도 분석이 필수적이며, eALS는 기존 ALS보다 K배 빠른 알고리즘이다.
데이터의 수가 증가하면 K를 높이는 것이 일반화에 유리하므로 대량의 데이터를 일반화하는 모델 학습에는 K배만큼 빠른 알고리즘이 좋을 것이라고 생각했습니다.
MF 공부를 계속하면서 시간 복잡도의 효과가 실제로 어떻게 느껴질지 실험해보고 싶다는 생각도 들었습니다.