4장 분류하는 뉴런 만들기-이진 분류

4-4 분류를 위한 데이터 세트 준비

– 유방암 데이터셋 생성

1. load_breast_cancer() 함수 호출

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

2. 입력 데이터 확인

print(cancer.data.shape, cancer.target.shape)


##출력: (569, 30) (569,)

3. 상자 그림으로 기능의 사분위수 관찰

cancer.data(:3)


##출력
array(((1.799e+01, 1.038e+01, 1.228e+02, 1.001e+03, 1.184e-01, 2.776e-01,
        3.001e-01, 1.471e-01, 2.419e-01, 7.871e-02, 1.095e+00, 9.053e-01,
        8.589e+00, 1.534e+02, 6.399e-03, 4.904e-02, 5.373e-02, 1.587e-02,
        3.003e-02, 6.193e-03, 2.538e+01, 1.733e+01, 1.846e+02, 2.019e+03,
        1.622e-01, 6.656e-01, 7.119e-01, 2.654e-01, 4.601e-01, 1.189e-01),
       (2.057e+01, 1.777e+01, 1.329e+02, 1.326e+03, 8.474e-02, 7.864e-02,
        8.690e-02, 7.017e-02, 1.812e-01, 5.667e-02, 5.435e-01, 7.339e-01,
        3.398e+00, 7.408e+01, 5.225e-03, 1.308e-02, 1.860e-02, 1.340e-02,
        1.389e-02, 3.532e-03, 2.499e+01, 2.341e+01, 1.588e+02, 1.956e+03,
        1.238e-01, 1.866e-01, 2.416e-01, 1.860e-01, 2.750e-01, 8.902e-02),
       (1.969e+01, 2.125e+01, 1.300e+02, 1.203e+03, 1.096e-01, 1.599e-01,
        1.974e-01, 1.279e-01, 2.069e-01, 5.999e-02, 7.456e-01, 7.869e-01,
        4.585e+00, 9.403e+01, 6.150e-03, 4.006e-02, 3.832e-02, 2.058e-02,
        2.250e-02, 4.571e-03, 2.357e+01, 2.553e+01, 1.525e+02, 1.709e+03,
        1.444e-01, 4.245e-01, 4.504e-01, 2.430e-01, 3.613e-01, 8.758e-02)))

4. 뛰어난 기능 살펴보기

import matplotlib.pyplot as plt
import numpy as np

plt.boxplot(cancer.data)
plt.xlabel('feature')
plt.ylabel('value')
plt.show()

5. 타겟 데이터 확인

cancer.feature_names((3,13,23))

##출력: array(('mean area', 'area error', 'worst area'), dtype="<U23")


np.unique(cancer.target, return_counts =True)

##출력: (array((0, 1)), array((212, 357)))

6. 학습 데이터 세트 저장

x = cancer.data
y = cancer.target

4-5 로지스틱 회귀를 위한 뉴런 만들기

– 모델 성능을 평가하기 위한 교육 세트 및 데이터 세트

규칙

1) 훈련 데이터셋을 분할할 때 훈련 데이터셋은 테스트 데이터셋보다 커야 합니다.

2) 트레이닝 세트를 분할하기 전에 양성 및 음성 클래스를 균등하게 혼합하여 트레이닝 또는 테스트 세트의 어느 한쪽에 군집되지 않도록 해야 합니다.

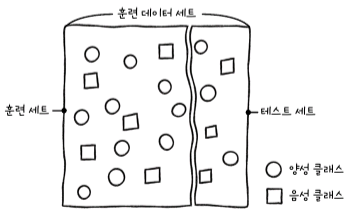
– 훈련 세트와 테스트 세트로 구분

1. train_test_split() 함수를 사용하여 교육 데이터 세트를 분할합니다.

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y, test_size=0.2, random_state=42)

2. 결과 확인

print(x_train.shape, x_test.shape)


##출력: (455, 30) (114, 30)

3. unique() 함수를 사용하여 훈련 세트에서 대상 식별

np.unique(y_train, return_counts = True)


##출력: (array((0, 1)), array((170, 285)))

※ 파라미터 설정 내용

– 로지스틱 회귀 구현

로지스틱 회귀에서 가중치를 업데이트하려면 데이터가 앞으로 흐르고 데이터가 뒤로 흘러야 합니다.

class LogisticNeuron:

  def __init__(self):
    self.w = None
    self.b = None

  def forpass(self, x):
    z = np.sum(x * self.w) + self.b    # 직선 방정식 계산
    return z

  def backprop(self, x ,err):
    w_grad = x *err                    # 가중치에 대한 그레이디언트 계산
    b_grad = 1 *err                    # 절편에 대한 그레이디언트 계산
    return w_grad, b_grad

a = np.array((1, 2, 3))
b = np.array((3, 4, 5))
print(a + b)
print(a * b)


##출력: (4 6 8)
##      ( 3  8 15)

np.sum(a * b)


##출력: 26

– 교육용 Besard 구현

1. fit() 메서드 구현

def fit(self, x ,y, epochs=100):
  self.w = np.ones(x.shape(1))  # 가중치 초기화
  self.b = 0                    # 절편 초기화
  for i in range(epochs):       # epochs만큼 반복
    for x_i, y_i in zip(x, y):  # 모든 샘플에 대해 반복
      z = self.forpass(x_i)     # 정방향 계산
      a = self.activation(z)    # 활성화 함수 적용
      err = -(y_i - a)          # 오차 계산
      w_grad, b_grad = self.backprop(x_i, err) # 역방향 계산
      self.w -= w_grad          # 가중치 업데이트
      self.b -= b_grad          # 절편 업데이트

2. activation() 메서드 구현

def activation(self, z):
  a = 1 / (1 + np.exp(-z))      # 시그모이드 계산
  return a

– 예측 방법의 구현

1. predict() 메서드를 구현합니다.

def predict(self, x):
  z = (self.forpass(x_i) for x_i in x)   # 선형 함수 적용
  a = self.activation(np.array(z))       # 활성화 함수 적용
  return a > 0.5                         # 계단 함수 적용

※ LogisticNeuron 클래스 요약

class LogisticNeuron:

  def __init__(self):
    self.w = None
    self.b = None

  def forpass(self, x):
    z = np.sum(x * self.w) + self.b    # 직선 방정식 계산
    return z

  def backprop(self, x ,err):
    w_grad = x *err                    # 가중치에 대한 그레이디언트 계산
    b_grad = 1 *err                    # 절편에 대한 그레이디언트 계산
    return w_grad, b_grad

  def activation(self, z):
    z = np.clip(z, -100, None)    # 안전한 np.exp() 계산을 위해
    a = 1 / (1 + np.exp(-z))      # 시그모이드 계산
    return a

  def fit(self, x ,y, epochs=100):
    self.w = np.ones(x.shape(1))  # 가중치 초기화
    self.b = 0                    # 절편 초기화
    for i in range(epochs):       # epochs만큼 반복
      for x_i, y_i in zip(x, y):  # 모든 샘플에 대해 반복
        z = self.forpass(x_i)     # 정방향 계산
        a = self.activation(z)    # 활성화 함수 적용
        err = -(y_i - a)          # 오차 계산
        w_grad, b_grad = self.backprop(x_i, err) # 역방향 계산
        self.w -= w_grad          # 가중치 업데이트
        self.b -= b_grad          # 절편 업데이트

  def predict(self, x):
    z = (self.forpass(x_i) for x_i in x)   # 선형 함수 적용
    a = self.activation(np.array(z))       # 활성화 함수 적용
    return a > 0.5                         # 계단 함수 적용

– 로지스틱 회귀 모델 교육

1. 모델 교육

neuron = LogisticNeuron()
neuron.fit(x_train, y_train)

2. 테스트 세트를 사용하여 모델의 정확도를 평가합니다.

np.mean(neuron.predict(x_test) == y_test)


##출력: 0.8245614035087719

※ 내용 배우고 조직하는 것.